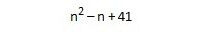Prime numbers. Is there a pattern? What about 1? What’s the highest prime?
The Continued Study
“Prime numbers are what is left when you have taken all the patterns away. I think prime numbers are like life.”
Prime numbers are one of the most beautiful things in mathematics. But also the most mysterious.
A prime number is only divisible by 1 and itself. For example, 2, 3, 5… 17… 97 are all primes. Composites are just the opposite.
There is no definite pattern for primes however, we can see that all prime numbers must end in 1, 3, 5, 7, and 9 (excluding 2), or else it would be divisible by two.
Back in the old days, a now old-dead Greek guy named Eratosthenes sort of created a pattern. He was a polymath: a mathematician, astronomer, poet, and music theorist. Eratosthenes came up with something called “The Sieve of Eratosthenes' which worked by eliminating multiples of known prime numbers, about 2,300 years ago. It is an efficient and quick way to find small prime numbers but can get complicated quickly. It looks something like this:
It eliminates all the multiples of prime numbers to 225 (15 squared, so nothing can be bigger or you may miss one).
You can also see that all multiples of two are gone, which is logical.
Anyways, there have been more patterns said to be true for finding prime numbers.
Leonhard Euler, one of the greatest mathematicians of all time, did actually come up with a formula for generating prime numbers. Well, not really. You might be familiar with this. The formula goes as follows:
Try it out. You may notice that the formula only works for numbers under 40. So again, yes it does work for small numbers, but isn’t suitable for calculating large prime numbers.
So, there really isn’t… a pattern. This will still remain a mystery in the world of number theory and math.
The Search for the Highest Prime
The largest known prime number (as of May 2023) is 282,589,933 − 1, a number which has 24,862,048 digits when written in base 10.
Why is there an “as of…”? Well, larger prime numbers are being found throughout the months and years.
There are even prizes for finding large prime numbers.
A one-million-digit prime number was found in 1999, and the finder received a US$50,000 prize!
There is also a slight pattern seen in large primes. From Wikipedia:
Many of the largest known primes are Mersenne primes, numbers that are one less than a power of two because they can utilize a specialized primality test that is faster than the general one. As of November 2022 (7 months ago), the eight largest known primes are Mersenne primes. The last seventeen record primes were Mersenne primes. The binary representation of any Mersenne prime is composed of all ones since the binary form of 2k − 1 is simply k ones.
So who knows? Give it a try and see what you may find.
There is a Simple Answer for 1.
The “special” number 1.
It is not prime nor composite.
It lies in the definition itself. One has positive divisors - 1… and 1. It’s just 1. The definition of a prime is that it must have 2 positive divisors.
So it’s not prime.
It’s not composite either, it is only divisible by itself - 1 and nothing else.
You can call “1” using these terms instead:
An odd number
A natural number
A rational number
A positive integer
A whole number
What about… zero, the hero?
Zero, the truth.
Some people think it’s prime, some composite. But what is the real answer?
Here is a great mini “chart” from Brilliant.org’s wiki.
Why some people say it's prime: Its divisors are 1 and itself.
Why some people say it's composite: It divides by 2, 3, 5 and so on
Why some people say it’s neither: It doesn’t divide by itself
Firstly, this is more logical than 1, as 0 can divide by 1 and 0, however, 0 divided by 0 is undefined.
Secondly… it does divide by 2, 3, 4, and 5… but it still can’t divide by itself!
Simply put, 0 is not prime or composite. You can’t divide 0 by 0!
So 0 is just like 1.
Infinite Primes
Are there infinite primes?
Here’s a theorem to prove it.
Euclid's theorem is a fundamental statement in number theory that says that there are infinitely many prime numbers.
It will be difficult to explain… heh heh, so here’s an explanation I found.
Consider any finite list of prime numbers p1, p2, ..., pn. It will be shown that at least one additional prime number not in this list exists. Let P be the product of all the prime numbers in the list: P = p1p2...pn. Let q = P + 1. Then q is either prime or not:
If q is prime, then there is at least one more prime that is not in the list, namely, q itself.
If q is not prime, then some prime factor p divides q. If this factor p were in our list, then it would divide P (since P is the product of every number in the list); but p also divides P + 1 = q, as just stated. If p divides P and also q, then p must also divide the difference between the two numbers, which is (P + 1) − P or just 1. Since no prime number divides 1, p cannot be in the list. This means that at least one more prime number exists beyond those in the list.
Primes go on forever, so who knows what we can find in the future.